Trigonometric Substitution Integration

Have you ever experienced true pain with calculus? Want to relive those horrifying moments? Well look no further! We're going to be integrating some functions which will require trigonometric substitution! Yaaaay…

The First Case:

Let's begin. The basic idea of integrating complex expressions is to just try a bunch of stuff and pray that one of those methods will lead you slightly closer to the solution than you started with. The first trick we'll use is the Pythagorean theorem. We're going to use x^2 + y^2 = z^2 as the values since "a" is already taken. Basically we're going to construct a right triangle, and that expression above is going to be the lengths of one of the sides. Then, we use the power of trigonometry to substitute in different functions that will actually be solvable. Plugging the above into the hypotenuse we get some nice values out of it:

It doesn't matter which variable we assign to which triangle leg. I'm setting it up like this. Now, use the triangle's properties to create equations that can be used to substitute values back in the original integral. We need a replacement for du and for that square root expression.

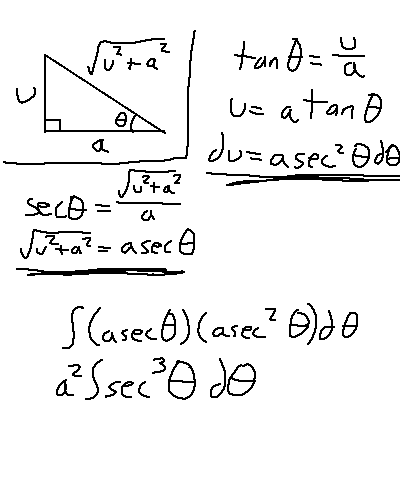
Alright, so now we just need to solve for that. Surprise, it's not easy. We'll have to pull out another trick: integration by parts. I'm not going to explain how integration by parts works. It turns out that sec^2(x) is easily integrable, so we'll use that as our "dv" value. the "u" value must be sec(x), then.

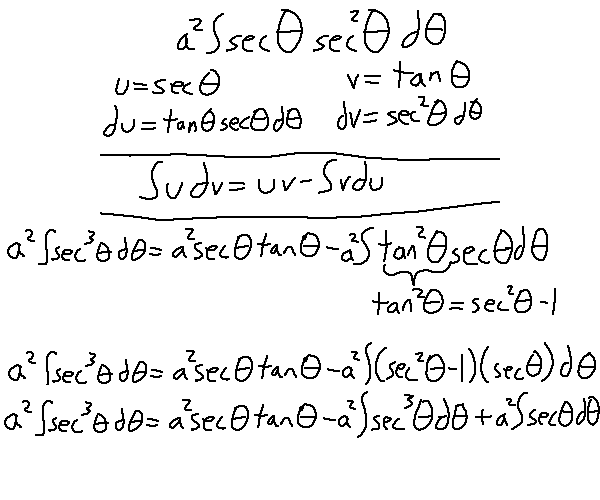
After using integration by parts and a trigonometric identity, we're left with this. We actually ended up with another copy of our starting place. This means we can combine that term with the left side of the equation and do some reduction, meaning that the last integral we need to care about is sec(theta). Just look this one up, honestly. It's another whole mess to figure this one out.

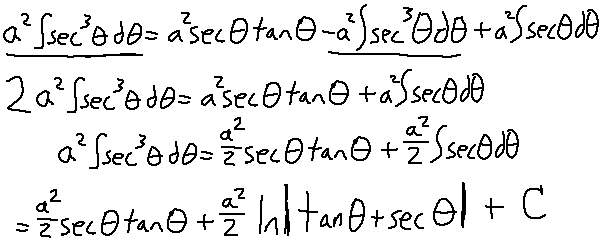
Now that no more integrals remain, it's time to resubstitute back the u and a variables! Remember the triangle we constructed from earlier to help us with this.

Note that near the end I used a property of logarithms to take out the (1/a) inside the log, then merging that value with C because they're both constants. And there's the first out of three forms. Oh yeah, there's two more problems in the set.

The Second Case:

Do a similar process for this case. Set up the triangle, and do some substitutions.

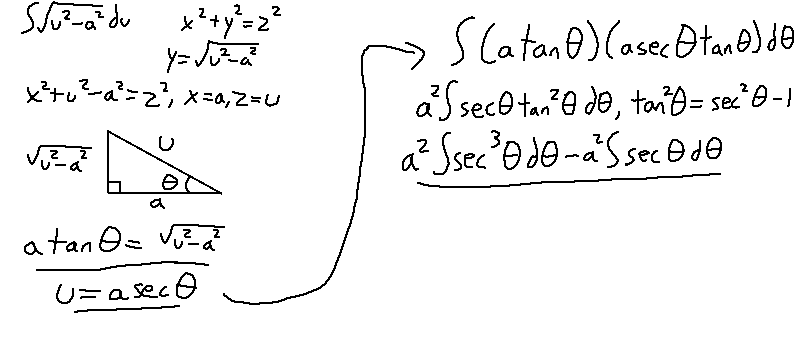
Wait, that term looks familiar… we already solved for sec^3(theta)! We solved for sec(theta) as well. The only difference is that the value of the sec(theta) integral will be negative. Well, that's convenient.

Alright! One more to go.

The Third Case:

The steps here are way easier: they just require different substitutions. For the last part, theta is by itself, meaning we'll have to go back to the triangle and find an equation that gets theta by itself.

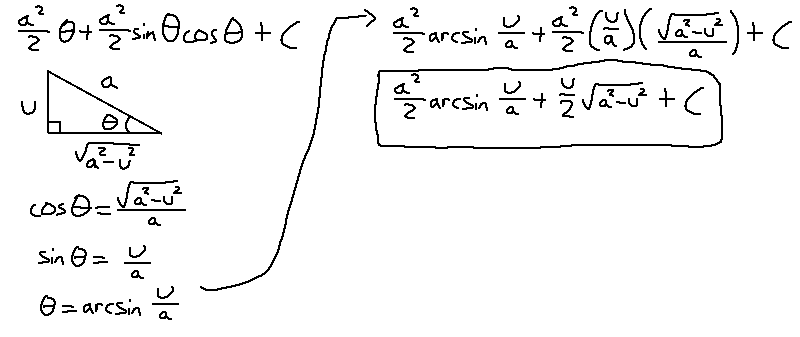
Aaaaaand that's how you do it.