Small Tricks the Sequel
Here's a few more unrelated things that may be cool or helpful.
Roots of Polynomials and its Derivatives
The nature of roots to polynomial equations have been an interest of mine for a while. Take a parabola, for example. The parabola always has this horizontal symmetry at the point where the slope is zero, right in its "center". It doesn't take much to look at a parabola and notice that if that parabola has any roots, their values will average to that x value at which the slope is 0. This is how you would write that algebraically:

How can we use this? Well, this means that we can always know what the average of all the roots are, as it only depends on setting the derivative of the quadratic to 0. Since there's really only one variable we need to calculate all the roots, which is the distance from this average number, the polynomial is solvable in a different manner. Observe:
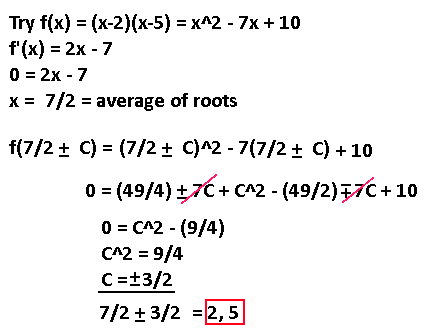
Using the plus-minus operation in algebra is a rare sight, but is useful in this situation. The way to read this equation is as two separate equations, one using the "top" operations and one using the "bottom" operations only. In both cases after expanding out, the 7C terms cancel each other out because of the -7 term flipping that sign. C^2 loses its plus-minus operation because it gets squared. Neat!
What about for higher powers? What happens when we use this same idea of setting the derivative to zero and compare it with the roots? Below is an example of a third-order polynomial
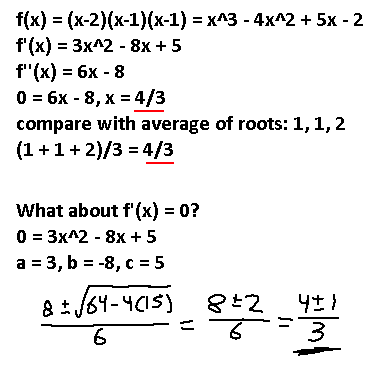
The roots of this polynomial are 1, 1, 2, giving an average of 4/3. Setting f''(x) to zero we get 4/3 as well. Furthermore, setting f'(x) to zero gives us two possible roots, but notice the hidden 4/3 value in there. It is 4/3, plus or minus 1, which makes the average of those values also 4/3.
The pattern seems to follow as this: given some f(x), the average of all of its roots are equal to the average of all the roots of the derivatives of f(x) down to its linear form.
Is there anything further to extrapolate from this? I'm not sure. I don't think you can use this knowledge to find the roots of any polynomial, for instance. After all, there is a limit to how many roots you can guarantee to find for any polynomial. It becomes not a guarantee anymore after a quartic polynomial by using just algebraic means. So, not all quintic functions are solvable using algebraic means. Check out the Abel-Ruffini theorem if you're curious.
I can't really prove it, but it SEEMS like each root found in a derivative function is a midpoint of two roots in the original fuction. For example, this function (x-1)(x-3)(x-5)(x+6) has an f'''(x) = 24x - 18. Setting that to zero shows that the average of all roots is 3/4. Going "up a level" and plugging in f''( (3/4) +- C ) will give us two other roots after solving for C, which ends us up with sqrt(275/48). In theory, you should be able to go up another level and plug in f'( (3/4) + sqrt(275/48) +- D) and get two more roots after solving for D, and also plug in f'( (3/4) - sqrt(275/48) +- E) to get yet two more roots solving for E. One of those roots found will be the same, since f'(x) is a cubic function and can only have a maximum of three roots, and you're finding four roots in total by solving those two equations above. Again, that's assuming my hypothesis is true, which I have a feeling it isn't. The algebra gets way too messy for my tastes.
Prime Estimations
Have you tried finding prime numbers using the Sieve of Eratosthenes? You take all the numbers from 2 upward and start removing composite terms, first finding all even numbers. The first number that survives the sieve is 3, so then you remove all terms divisible by 3. 5 is the new first term you're left with, so then you remove all terms divisible by 5, and so on. Let's say you only removed all the even numbers. So, you have 3,5,7,9,11. The primes are correct up until 9. That's what the 3 filter is for, and when you do that you get 5,7,11,13,17, etc. Everything looks like they're prime again until you hit 25. That's what the 5 filter is for. Notice the pattern yet? If you perform this sieve pattern up to prime number N, your first inaccuracy will happen at the next prime number squared.
There is another trick that is similar to this topic to finding primes. It's essentially a probabilistic equation, where all the primes possible are within a shorter sequence than just looking at all the positive numbers. An easy example is the odd numbers: all primes excluding 2 are findable in the odds, so you "only" need to look at half the natural numbers for primes. Can we do better? Definitely.
The trick is to understand the cyclic nature of this sieve, and how some are prime and some are composite. When filtering out all numbers divisble by 2, you end up with a cyclic pattern of 2, where you ESTIMATE that half the numbers are prime and half are not. We'll call this pattern P,C, where P means prime and C means composite. You can get more accurate by filtering out 2 and 3 factors in numbers, and you'll end up with this pattern: P,C,C,C,P,C. This is a cycle pattern that you can start at 7, which is prime, and the next three numbers are composite, followed by a prime, then a composite. This cycle continues and weeds out 2/3 of all the numbers you need to check, since this cycle shows that 4 are guaranteed to be composite out of 6. The inaccuracy starts after 25, which is what we learned already. Below demonstrates this.
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 ...
P C C C P C P C C C P C P C C C P C P
These two primes out of 6 pattern can be converted into equations like so:
f(x) = 6x + 1
g(x) = 6x + 4
Plug in any integer for x and you'll get out something that's PROBABLY a prime. It will get more inaccurate as x increases, which is why we need extra filter terms. Let's try adding 5 in. Turns out that the resulting pattern length jumps up from 6 to 30. Here's the pattern of that, starting at 31:
P,C,C,C,C,C,P,C,C,C,P,C,P,C,C,C,P,C,P,C,C,C,P,C,C,C,C,C,P,C
Looking at this pattern, our prime detecting accuracy increases from 1/3 being prime to 8/30 being prime. Here's one equation you could use that's more accurate:
f(x) = 30x + 1
The pattern length can be predicted by just taking all the prime numbers you're using to filter and multiplying them together! 30 is just 2*3*5. So, if we added 7 to the filter, the cycle length will jump up to 210. Yikes. And we know we will get inaccuracies starting at 11^2 = 121, which is before our first cycle even finishes. The equation you could use to detect this even more accurate method is f(x) = 210x + 1.
You could just multiply a ridiculous number of primes together and get some result P, then use f(x) = Px + 1 to get a somewhat accurate detector of primes this way... up until 2*3*5*7*11*13. Then the number for addition needs to change. I cannot prove it, but it seems like the number to add must make this function return a prime for x = 1, or else none of the numbers in the sequence will be prime. This is the highest I got to manually before stopping myself: f(x) = (2*3*5*7*11*13*17*19*23*29*31) + 67. This one is a prime for x = 1.
Extending the Babylonian Method
There's a way to iteratively approximate the square root of a number, and that's using the Babylonian Method. What you do is specify a number to take the square root of and call it x0. Then, use this definition to compute higher terms of x until you're content with your approximation:
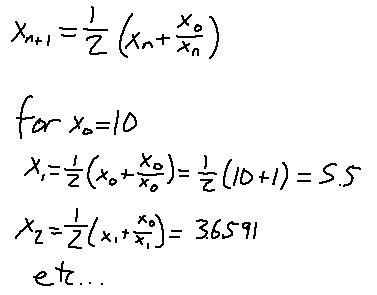
What about cubed roots and quartic roots? The formula slightly changes:
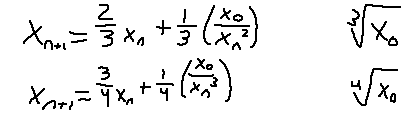
I spy a pattern. You can consider the coefficients as "weights", as they always add up to 1. As the root number grows, more weight is shifted to the xN term and less on the fraction. Here's what you can use if you want to calculate the ath root of a number iteratively:
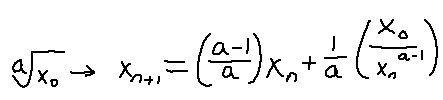
If the weights are wrong, then it may still converge to the value you desire, but it will either converge more slowly than it could, or it will oscillate around the value!
Pascal Triangle's terms
There is another way to represent the terms of each row in Pascal's Triangle. I will show a way in which you can figure out the next term by multiplying the previous term by some number. Below is for the 4th row:
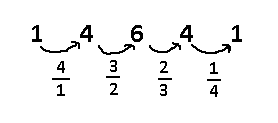
You start with 4/1, then multiply the first term by that. For every term after that, you take one out of the numerator and add one to the denominator, then multiply by that, until you get to the end. For row N, start on N/1, and do the same trick until you get to 1/N.
What's cool is that despite multiplying by all these fractions, you will always end up with a whole number after every multiplication. How is that possible? It has to do with the incremental and decremental nature of our chosen fractions.
Imagine you have all the integers in a number line, but you're unable to actually see what the numbers are. How can you guarantee that you'll find an even number? If you pick two numbers next to each other, one of them has to be an even number, because every other number in the line is going to be even. As for numbers divisible by 3, you just pick three numbers consecutively on the number line, and one of them has to be divisible by three.
So, focusing on only the denominators of these multiplied fractions, notice that we don't divide by N until the Nth fraction. So, we don't divide by 3 until the third term. At the same time, notice how the numerators all have integers that are next to each other on the number line. After the second term, you'll be guaranteed to find a number divisible by 2, and after the third term you'll be guaranteed to find a number divisible by 3, and so on. So, because by term N you'll be guaranteed a number divisble by N, that's why dividing by N at that point will always net you a whole number.
That's all for now!