Polynomial Construction from Sequences III

To warn you, this is going to be a little detour from the series. You don't need to read this one to understand future posts, and it's going to be a lot more difficult.

Look at the diagonals of Pascal's triangle, so that you get sequences of (1,2,3,4,…), (1,3,6,10,…), (1,4,10,20,…), etc. Using the formulas generated earlier, we can find out the polynomial expressions that would produce these values. Here are the first few of them:

            
x
(1/2)x^2 + (1/2)x
(1/6)x^3 + (1/2)x^2 + (1/3)x
(1/24)x^4 + (1/4)x^3 + (11/24)x^2 + (1/4)x

            
        

Notice that in all of the above expressions the coefficients add up to 1. Is there a way to predict the next pattern? Maybe it would help if the coefficients were organized into yet another Pascal's triangle?

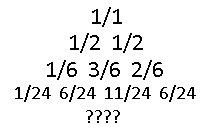
Here's the first few rows of the coefficients. I made all the denominators the same for each row to make things easier to understand. To reiterate, for each diagonal in Pascal's triangle we are looking for a polynomial which would output that sequence, then taking the coefficients of that polynomial and putting them into another triangle formation. This is going to get really difficult, so what I ended up doing is writing a program that does it for me. I used Haskell for a few reasons, the main one being it's the only language I can program in with built in rational number support. I dont want my fractions to coerce into an integer or a float the moment I try to do anything with them. Here's the code if you want it for your own nefarious reasons:

            
import Data.Ratio

input :: [Rational] 
input = [1,2]

main = do
    print $ prettyPrintFormula $ findFormula input

findFormula :: [Rational] -> [(Rational, Integer)]
findFormula sequence = cycleInput [] sequence

prettyPrintFormula :: [(Rational, Integer)] -> String
prettyPrintFormula terms = cutLastAddition $ foldr (++) "" (map prettyPrintTerm terms)

cutLastAddition :: String -> String
cutLastAddition str = reverse $ tail $ tail $ tail $ reverse str

prettyPrintTerm :: (Rational, Integer) -> String
prettyPrintTerm (r, p)
    | d == 1 && p == 0 = show n ++ " + "
    | d == 1 = show n ++ "x^" ++ show p ++ " + "
    | p == 0 = "(" ++ show n ++ "/" ++ show d ++ ")" ++ " + "
    | otherwise = "(" ++ show n ++ "/" ++ show d ++ ")x^" ++ show p ++ " + "
    where 
        n = numerator r
        d = denominator r

cycleInput :: [(Rational, Integer)] -> [Rational] -> [(Rational, Integer)]
cycleInput terms sequence
    | isAllZero sequence = terms
    | otherwise = cycleInput newTerms (subtractTermsFromSequence newTerms input)
    where 
        term = antiDerivativeOfConstant $ findConstant (sequence, 0)
        newTerms = terms ++ [term]

subtractTermsFromSequence :: [(Rational, Integer)] -> [Rational] -> [Rational]
subtractTermsFromSequence terms sequence = map (subtractTermsFromNumber terms) (zip [1..] sequence)

subtractTermsFromNumber :: [(Rational, Integer)] -> (Integer, Rational) -> Rational
subtractTermsFromNumber terms (value, number) = number - (evaluateTerms terms value)

evaluateTerms :: [(Rational, Integer)] -> Integer -> Rational
evaluateTerms terms value = foldr (+) 0 (map (evaluateTerm value) terms)

evaluateTerm :: Integer -> (Rational, Integer) -> Rational
evaluateTerm value (coeff, power) = coeff * fromInteger (value ^ power)

antiDerivativeOfConstant :: (Rational, Integer) -> (Rational, Integer)
antiDerivativeOfConstant (num, count) = ( num / fromInteger (factorial count), count)

factorial :: Integer -> Integer
factorial 0 = 1
factorial 1 = 1
factorial n = n * factorial (n - 1)

findConstant :: ([Rational], Integer) -> (Rational, Integer)
findConstant ((x:xs), count)
    | isAllSame (x:xs) = (x, count)
    | otherwise = findConstant (subBetweenNumbers (x:xs), count + 1)

subBetweenNumbers :: [Rational] -> [Rational]
subBetweenNumbers (x:y:[]) = [y - x]
subBetweenNumbers (x:y:xs) = (y - x) : subBetweenNumbers (y:xs)

isAllSame :: [Rational] -> Bool
isAllSame (x:[]) = True
isAllSame (x:y:xs) = (x == y) && isAllSame (y:xs)

isAllZero :: [Rational] -> Bool
isAllZero (x:[]) = x == 0
isAllZero (x:xs) = (x == 0) && isAllZero xs
            
        

Now with the power of computers, I bring to you the next few rows of this weird triangle!

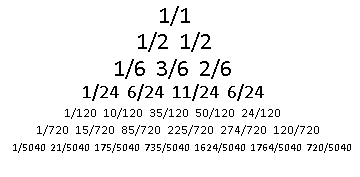
Those denominators are pretty annoying. I'll just make a note of the value of the denominator for each row. There is an additional way to simplify it, as those denominators are factorial values!

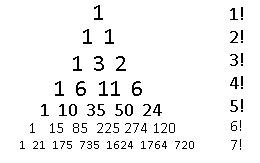
The left side of the triangle is all 1's, just like in Pascal's triangle, but the numbers on the right side are all factorial numbers! Our next hint is noticing that the numbers down the right diagonals are all expanding at a factorial rate, just like the right side of the triangle. From there we can find some patterns, so now I'm going to look at each diagonal column from right to left and show how to get to the next value

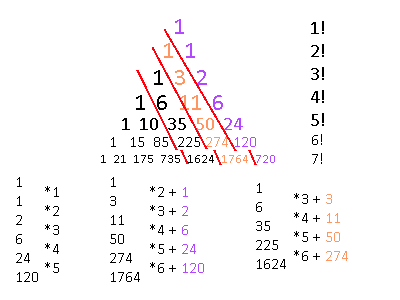
It is here where an interesting revelation is found. Pascal's triangle could be defined recursively where the next row was dependent on the calculations of all the previous rows. However, with this triangle It seems that the only set of numbers which don't have any such dependencies is the right-most diagonal set of numbers on the far right, the factorial numbers! The second diagonal row, 1,3,11,50,274, also increases factorially, but with an extra addition which involves the term on its right, as I've noted above with the colors.

Unfortunately, because of that extra addition term, there isn't really a nice formula where you can just plug in some number and get the nth term in the row like with pascal's triangle. Maybe there is, but for now I'm leaving it at this recursive form.

What's a good way to represent this recursive form? Well, since the initial values don't start at a point like Pascal's triangle, then the top of this structure should actually be flat, which contain all the factorial values. So, what we want isn't a triangle form, but a sort of square which expands infinitely to the right and to the bottom.

Well, that's kind of a mess. What was the reason we did all this again? Oh yeah. The numbers that this grid creates are the coefficients to polynomial formulas which help us construct Pascal's triangle one diagonal row at a time, instead of calculating it by one horizontal row at a time. We now know that each diagonal row of pascal's triangle requires polynomials of higher powers as we go down those diagonal rows, and that the coefficients of those polynomials show a factorial growth. Not exactly an efficient or intuitive way to find a specific point in Pascal's triangle, but we did get a sweet program out of it, and that program will be what is used to revisit the generalized term formulas found in the previous post of this series.