Polynomial Construction from Sequences I

A long time ago I figured out a neat trick where given a sequence of numbers, you reverse engineer a formula which spits out those numbers. This trick involves taking repeated differences between each of the numbers. Let me show you how it works.

Let's say you have the numbers 1,2,3,4,5. The change in value across the sequence is always an increase by 1. You can consider this as the "slope" of the sequence. If we looked at 3,6,9,12,15 instead then this slope value is 3, and when you try to figure out an equation that outputs that sequence from x=1 onward you'll get f(x) = 3x. Constant change over the numbers is easy: find a slope value M, and the resulting equation is f(x) = M*x + C.

What isn't so easy is something like 1,4,9,16,25. Taking the difference between each of the numbers you'll see that the difference itself increases. It goes +3, +5, +7, then +9. This is where we apply the technique again but to the difference numbers. The following is an effective way to visualize what will be the whole process of what we're doing here: taking differences of differences until we find no more changes in the numbers.

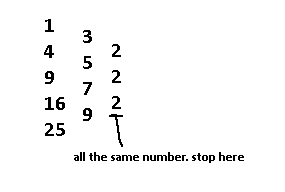
So, constant numbers were found 2 layers deep. This layer number is significant, as it gives key insight into what kind of polynomial that sequence represents. In this case, a 2 layer difference means a 2nd order polynomial. This means the equation we are looking for which matches this sequence is Ax^2 + Bx + C.

Just like the slope value in the first sequence is important, the slope value of "2" in this sequence is also important. Since this value represents a change in the 2nd order, this value directly relates to the coefficient for the polynomial term Ax^2. In order to find that A value, you have to take two antiderivatives of "2". For those that don't know calculus, this basically means that for N antiderivatives, you have to divide your number by 1, 2, 3, 4, …. all the way to N, and the x will have an exponent of N as a result. Check below for a visual demonstration.

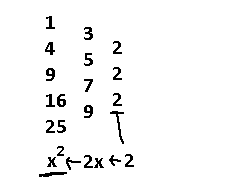
It turns out that x^2 perfectly matches the sequence 1,4,9,16,25, and beyond, assuming we start at x = 1. But unfortunately, this was a lucky case. What about a sequence like this?

3,6,13,24,39

Let's apply the difference of differences tactic and see where this leads us to.

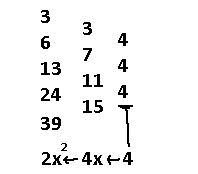
To recap, we took the differences between numbers until we hit the constant "4". Then, we applied 2 antiderivatives since the differences ran 2 layers deep, resulting in an x^2 term and dividing the "4" by 1, then by 2.

This first term is definitely 2x^2. But, this alone does not output the correct sequence. There is a missing x term and constant term still! How do we find those values? Think about it like this: you have some unknown 2nd order polynomial Ax^2 + Bx + C. You know that A is 2. In order to find the whole thing, what you can do is subtract the known Ax^2 term out of the unknown part, leaving you with Bx + C. Then, you can use the difference of differences trick to solve that subpart!

So, what will happen next is extracting the sequence out of 2x^2 for x = 1,2,3,4,5. Then, we take those values and subtract our starting sequence by them to give us what will be essentially Bx + C, the unknown part.

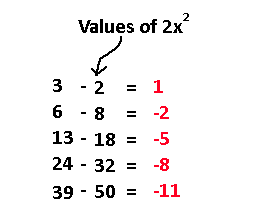
That red sequence is what we'll use now! It's okay to have negative values. Just remember that if you subtract a negative number that it turns into addition.

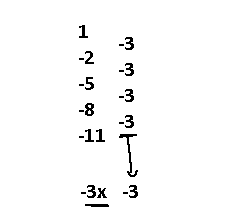
Applying what we did for the first sequence, we get our mythical Bx term! So, our known formula is now 2x^2 - 3x. If you extract the sequence out of this formula you'll end up with -1,2,9,20,35, and that looks really close to our target 3,6,13,24,29. We can inspect from here that if our known sequence had their values shifted up by 4 then we would get a perfect match. Therefore, the elusive C value is easily found as 4, making our final formula 2x^2 - 3x + 4.

There are a few takeaways from this. In reality we do not need some of the numbers in the starting sequence to figure out the equation. For a 2nd order polynomial it turns out that 3 terms are all that's needed, and that 2 terms are all that's needed to find a linear equation. If you have N terms in some sequence, then by going through this process the maximum order polynomial you can get out of that sequence is N-1. Note that if the original sequence is something that is not a polynomial, then you will not be able to find that equation, you will just find an approximation polynomial formula; so, this doesn't cover geometric sequences whose terms double each time, or cyclical sequences which imply the original equation has a sine, cosine, or exponential form to it. One last thing is that this will all still work if the coefficients of the polynomial you are finding are fractions. Things get a little messy there.

I will now give a more full example of the entire process in action, but with a more difficult sequence.

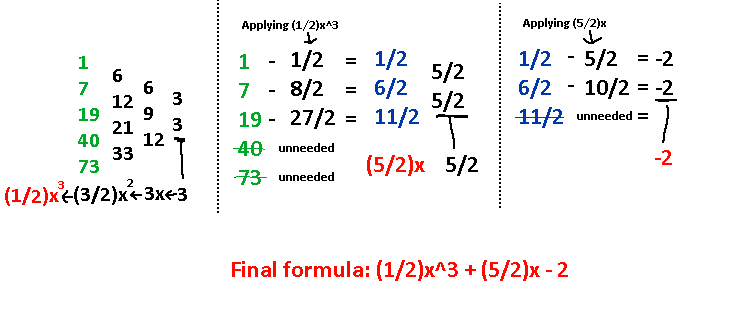
There is a lot more that can be uncovered with this technique, but I will save it for another time! Why not try it out and find the formula of the triangle numbers? 1,3,6,10,15…