Perimeter of an Ellipse
The perimeter of a circle is simple. 2 Pi radius, or Tau radius for the Pi non-believers. An ellipse is much harder, strangely enough. We can get approximations or use infinite series to get close though. I want to make my own approximation.
Much like how a circle can be described in terms of sine and cosine functions, an ellipse can also be described in such functions by using parametric equations. It is a sort of periodic motion to look at the change in radius over the change in angle for an ellipse. For a circle the radius is constant, but for an ellipse it rhythmically transitions between two values: the major axis and the minor axis. A sinusoidal function could model that behavior pretty well. Here's what we're looking for.
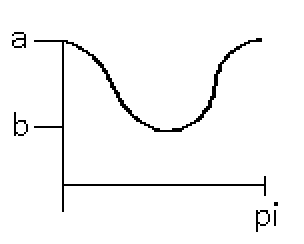
After going halfway around the ellipse starting from the major axis a (pi radians), we should get back to the radius of a. Looks good! Time to model this curve. The mid-point of the curve is at (a+b)/2 so that should be the y-offset value. As for the sine's amplitude, it is the difference between a and b, divided by 2. Something like this should work:
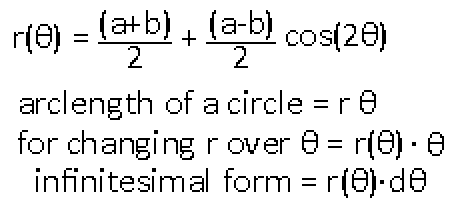
If you are confused by the arclength formula I have made another post about this stuff: "Angles! Circles! Integrals!" Anyway, time to plug this into an integral. I'm just going to integrate from 0 radians to pi / 2 radians, which is a fourth of the total perimeter of the ellipse. I can then just multiply the result by 4 to get the full perimeter, taking advantage of the ellipse's symmetry.
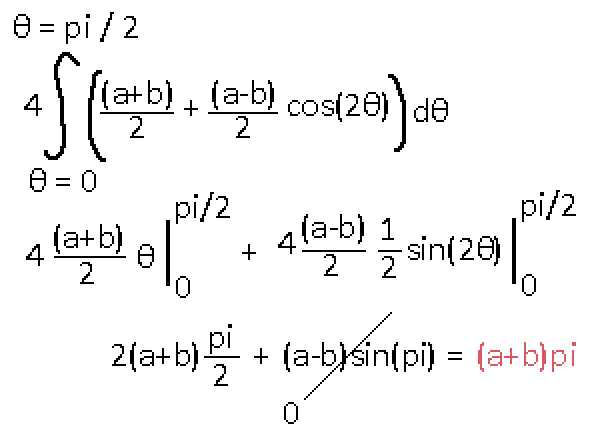
Uhmm.. wait. The sinusoidal component vanished. This result seems like a poor estimation. Let me check my python estimator program real quick.
Ratio 1:1 -> 0.0
Ratio 2:1 -> 2.7214911384786356
Ratio 3:1 -> 5.974777299140367
Ratio 4:1 -> 8.444911665224181
Ratio 5:1 -> 10.283122503947945
Ratio 10:1 -> 14.966194030716592
Ratio 100:1 -> 20.696560827945515
Ratio 1000:1 -> 21.381950220513023
Ratio 10000:1 -> 21.45233364395672
This log output shows different ratios of major axis to minor axis for ellipses. A ratio of 1:1 is a circle, 2:1 means the major axis is twice as large as the minor axis, and so on. The number on the far right is the percentage of error from the actual perimeter of the ellipse. Looks like it quickly loses accuracy up to a maximum of about 21.5%. Well that won't do.
Oh wait. I know why the sine part vanished. Take a look at the range I integrated the curve over.
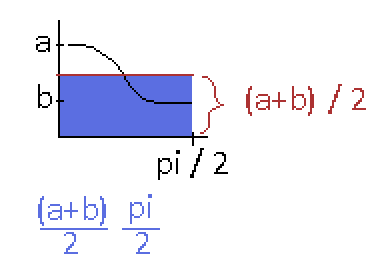
The black line is the full equation of the integration. But really it's just a regular cosine curve offset by a constant amount in the y direction. That constant offset is represented by the (a+b) * pi result we got. It turns out that offset is the only contributing factor in the sum. Look at how the black line has a positive and a negative sum if we set our x = 0 on the red line. They perfectly cancel each other out. The blue colored area accounts for all of the area under the black line curve here, and if you multiply that sum by 4 you end up with our (a+b)*pi we got.
Well I would very much like the whole point of my approximation to not be excluded during integration. I will need a sinusoidal function that won't cancel itself out in the end. How about this instead?
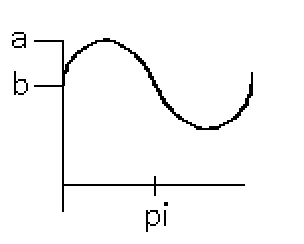
This is different than the first curve. Instead I will start at b at the sine's inflection point instead of the minimum, and the apex of the curve will be at a. This summation will definitely not cancel out this time. What will this equation look like?
There is a slight problem where after pi the value tends to negative a. This is fine, as we will only integrate the first quarter of this curve's period before negative values become an issue. Time to evaluate the integral!
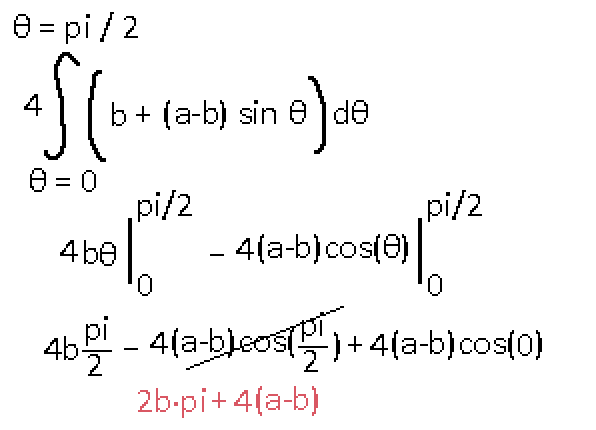
Looks interesting. Time to check out its accuracy.
Ratio 1:1 -> 0.0
Ratio 2:1 -> 6.138620686133895
Ratio 3:1 -> 6.87092722306222
Ratio 4:1 -> 6.564970727644871
Ratio 5:1 -> 6.0596766707731415
Ratio 10:1 -> 4.043931957584005
Ratio 100:1 -> 0.5431889335909049
Ratio 1000:1 -> 0.05668970914099061
Ratio 10000:1 -> 0.005702914662623921
Wow, that is pretty good. Not only is it completely accurate in the circle case, but it also tends to perfect accuracy in the infinitely stretched ellipse case. If you squished the ellipse into just a line, no minor axis, this equation would also perfectly estimate the length. If b is 0, this equation gives 4*a which is correct. In the circle case where a = b the equation is 2*pi*a which is also correct!
How do other approximations compare? I'm going to find some and test that out. Oh hey, here is a cool website. Let's test some of these out.
Mathisfun Approximation 1
Ratio 1:1 -> 0.0
Ratio 2:1 -> 2.5405517957602495
Ratio 3:1 -> 5.123394779339265
Ratio 4:1 -> 6.770663161677988
Ratio 5:1 -> 7.826267362178979
Ratio 10:1 -> 9.868859763728075
Ratio 100:1 -> 11.047135326462605
Ratio 1000:1 -> 11.071696140675124
Ratio 10000:1 -> 11.072068402048957
It has better accuracy up until 4:1 ratio, then it gets worse.
Mathisfun Approximation 2
Ratio 1:1 -> 0.0
Ratio 2:1 -> 0.0002799506770339681
Ratio 3:1 -> 0.003392719357572033
Ratio 4:1 -> 0.010710699140453544
Ratio 5:1 -> 0.02113408342030678
Ratio 10:1 -> 0.08419496372671514
Ratio 100:1 -> 0.34202806381224116
Ratio 1000:1 -> 0.40687616803887355
Ratio 10000:1 -> 0.41461766387098115
Wow, that is a more complicated formula, but it is much better for most practical cases. However, over strectched ellipses of around 100:1 ratio my estimation wins. Although not really practical, the formula I came up with is the only one so far that gets more accurate the more stretched the ellipse gets.
Mathisfun Approximation 3
Ratio 1:1 -> 0.0
Ratio 2:1 -> 4.5596464458697937e-08
Ratio 3:1 -> 3.297658506027773e-06
Ratio 4:1 -> 2.4992311356206883e-05
Ratio 5:1 -> 8.514084598049154e-05
Ratio 10:1 -> 0.0011557672353010313
Ratio 100:1 -> 0.02389769534904843
Ratio 1000:1 -> 0.03784219942767823
Ratio 10000:1 -> 0.039977305521903164
This one blows all other estimations out of the water. It only starts to get more inaccurate than mine around a ratio of 2000:1
I guess if I need to crudely estimate an ellipse's perimeter I could memorize 2*pi*b + 4(a-b) relatively easily.