Infinite Series and the Riemann Zeta Function

It's time to delve into new depths of insanity! This time, we'll be looking at the Riemann Zeta Function and how we could ever hope to derive some of it using our primitive minds.

I'm going to warn you right now, so I don't get yelled about it later. What we are about to do is not the conventional way of doing math. The main problem is that I'm going to associate the sums of infinite series with finite values, despite said infinite series clearly diverging to infinity. We are going to be using Ramanujan summation to help us with this problem, but just realize that when I use the "=" sign for these series that should diverge, it is a statement of assignment and NOT equality. Okay! Let's continue.

For those that don't know, the Riemann Zeta function is defined by summing the reciprocal of the natural numbers raised to some power. Here's what it looks like:

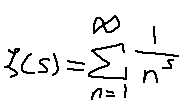
If you plug in s = -1, you'll end up getting a sum of 1 + 2 + 3 + 4, etc… aka the natural numbers. What's going to be strange is that we are going to be able to extract a finite number out of sequences like this. Perhaps some of you even know what we're going to end up with. But the important part is understanding how we get there.

Let's start with the basics of this concept. We are going to extract a finite value out of this sequence: 1 - 1 + 1 - 1 + 1 - 1 …. It looks like the value should only be either 0 or 1, and you're right. But, if we have two of these sequences, we can shift them in a certain manner that causes the infinite series to become finite. Observe.

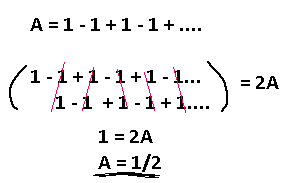
We added this sequence by itself, so we have 2A total. We shift the second infinite series by one to the right, and by performing addition with the terms above it we see that all future terms cancel each other out perfectly, leaving us with 1! The answer, then, is 1/2.

This is a prerequisite for the next sequence, which you will understand why soon. Now assign a value to 1 - 2 + 3 - 4 + 5 - … Use the same trick as before.

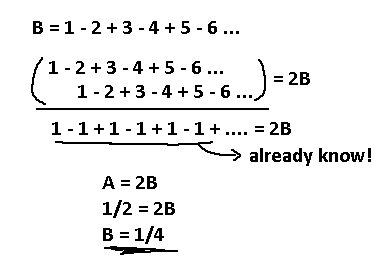
We ended up with our already solved sequence, so replace that with 1/2, our answer from before. Now we assigned 1/4 to this alternating sequence!

We built up a couple relations, and now we can finally tackle that natural number sum. We are going to do something slightly different this time, since we're dealing with non-alternating terms.

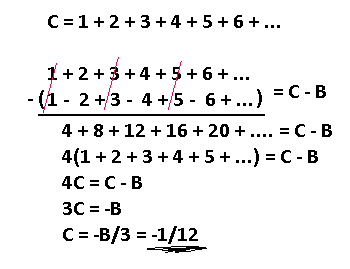
Interesting. By using our B sequence we cancelled out all the odd terms, leaving just the even terms being added. The result is just our original sequence times 4, so we can assign that to C again and solve from there.

Before we get too far, I'm going to standardize the notation a bit. I'm going to reuse the sigma symbol to define these infinite sequences. They come in two flavors, one with alternating signs and one without alternating signs. See below for examples.

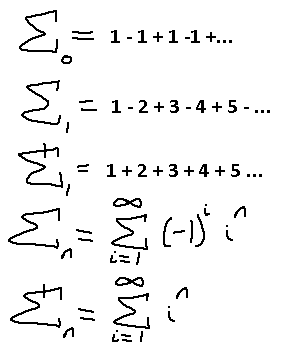
Cool. What about higher power sequences? Let's find out for when n = 2. Use the same procedure as before.

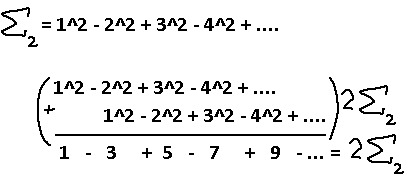
What's this now? A new sequence we need to find the pattern of? Oh wait, I did like, a whole series on solving sequences like this. Heh, This is nothing. Ignore the alternating signs for now.

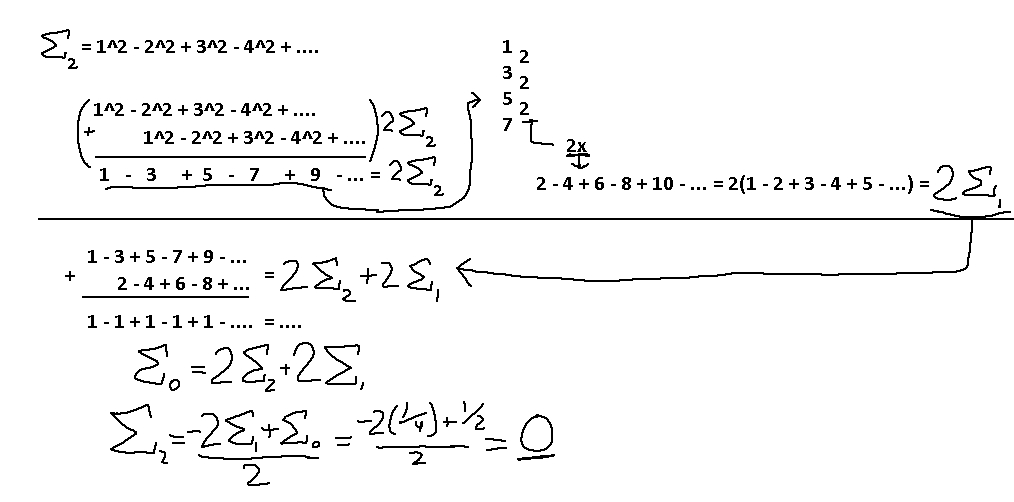
So, what we did is find a way to reduce the sequence 1 - 3 + 5 - 7 + … into something that's a constant by using the infinite sequences we already knew the values to. Once we ended up with 1 - 1 + 1 … we already knew the value assigned to that sequence, and can fully solve for the alternating square series! We get a… zero? Interesting. I wonder how that will affect the result of the positive square series.

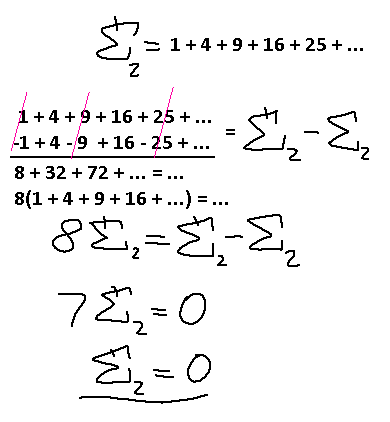
Ah. The only other unique term was that E2 term, which is zero anyway, so that makes the positive square series zero as well.

What's pretty cool is that after doing a bit of this, a pattern shows, and all we really need to solve the positive power integers (1^n + 2^n + 3^n + …) is to take its alternating sign counterpart and combine the two series together to blast half the terms out, then find the original series in that result and isolate the series by itself. Don't believe me?

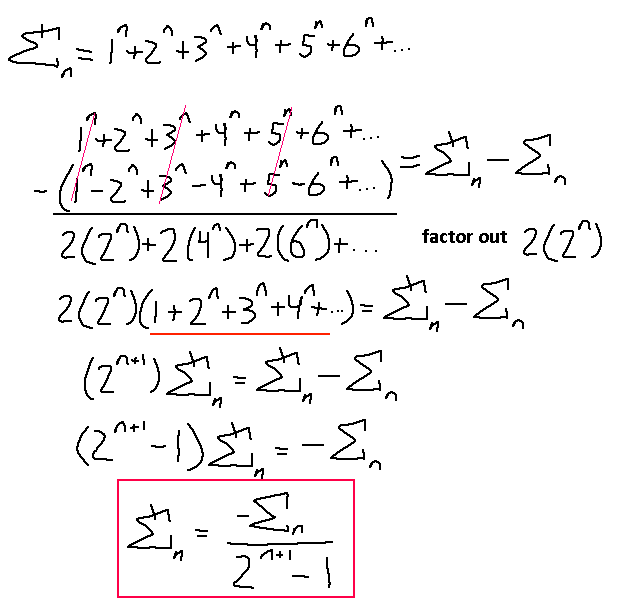
Here it's easier to see why our sums of squares became 0. The only real dependencies are the alternative sign series results and the power N.

Oh yeah, we can go back and solve the sums of a series of 1's, all positive. We haven't done that yet. Let's use this generalized formula for this.

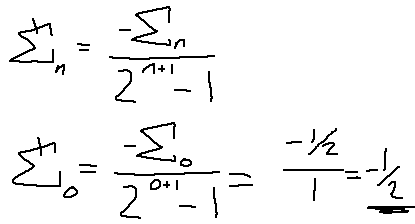
Alright! So we solved half of the problem… I guess. Here's what we have so far:

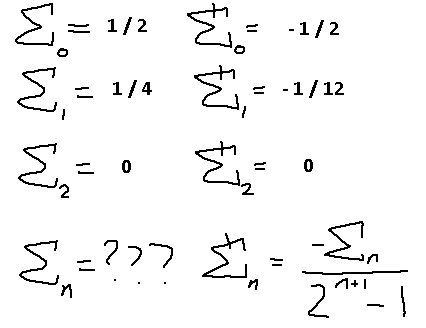
We just need to find a general form for the sums of alternating sign integers to a power and we have a solution. Keep in mind that this solution is only for positive N integers. How does this relate to the riemann zeta function again? Well that function used the reciprocal of the powers of integers. If we wanted to translate what we learned from here into that function, we would just make N negative. So, if you plugged in 0 to the reimann zeta function you would get out -1/2, just like what we found here. You have to plug in -1 instead of 1 to see our -1/12 result, and plug in -2 instead of 2 to see our 0 result.

Alright, now we're going to find a way to describe the alternating sums of powers of integers (1^n - 2^n + 3^n - 4^n +…).

I'm going to go through the alternating cubes of integers and show how much more involved this is than the alternating squares of integers.

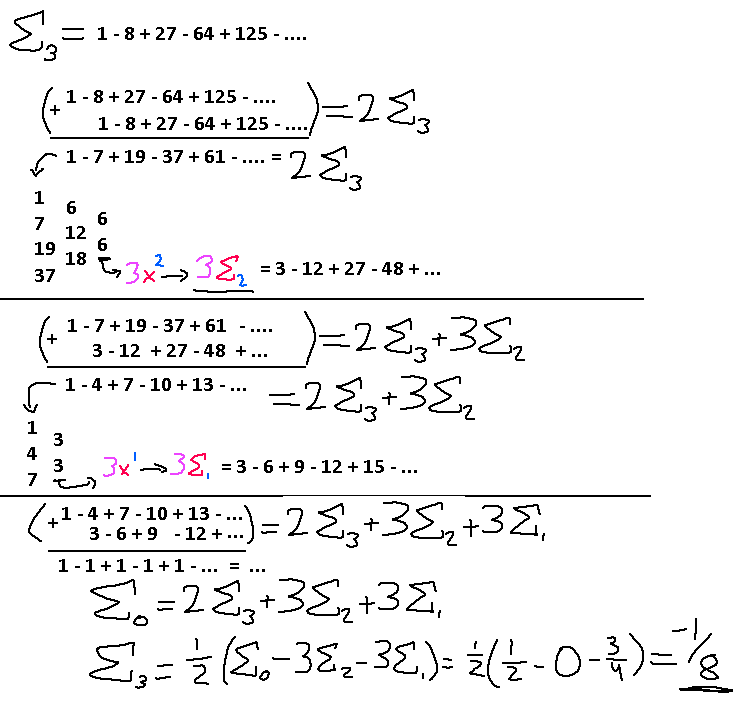
Using our differences trick we are able to find exactly the highest power term needed to reduce the infinite series back down to a linear growth, and yet another time to get all alternating 1's. I color coded those highest terms so you could see the relationship between the term we ended up with and the corresponding infinite series we need to use to reduce our problem down.

At this point you get the idea. The problem is trying to find a pattern out of all of this. A pattern really doesn't start showing up until E4 or E5. I'm going to spare the details and just jump straight to the last couple steps of finding those values. Perhaps you'll see something.

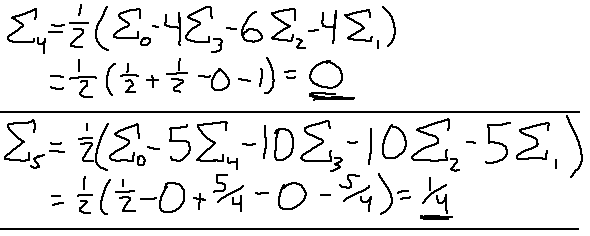
The final values themselves don't really reveal anything, other than the fact that all the even numbers evaluate to 0. What is important, however, is the last step before performing all the substitutions. I see pascal's triangle numbers hidden within there! Those numbers just sneak up everywhere, I swear.

Looks like the number N correlates to the Nth row of the triangle, so 5 leads to 1, 5, 10, 10, 5, 1. Looks like only the middle terms show up in each of these sequences. This shouldn't be too difficult to turn into a generalized form.

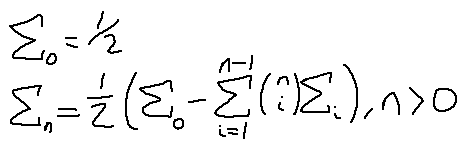
There we go. E0 is always going to be there, as well as the one half, and we compute the coefficients in the summation term there along with which EN to use for each term. This is a recurrence relation, as expected. So, we need to know all the previous terms before calculating the newest term. We will test this out and compare it to the riemann zeta function, but first we got to combine the two halves together; remember that this formula doesn't produce the riemann zeta values, that other function that we figured out in the last post will, in combination with this one.

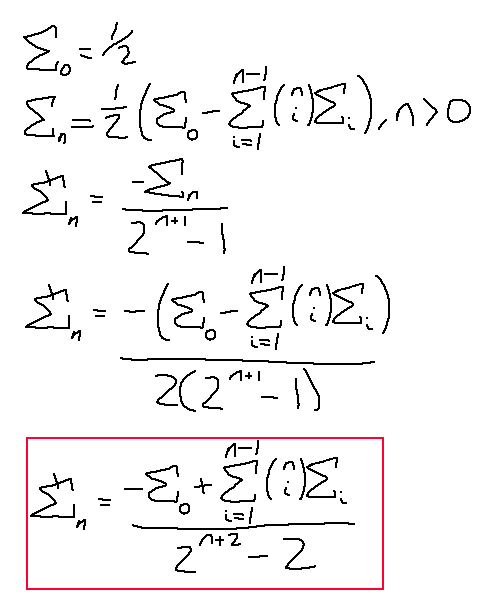
Note that this expanded form doesn't hold for N = 0; it needs to be specified that plugging in N = 0 spits out -1/2 as a base case, as well as E0 being 1/2.

Remember how this relates to the Riemann zeta function? We were dealing with the sums of integers instead of the sums of inverse integers, so to map this to that function we just flip the sign of N. Plugging in 7 to this equation is like plugging in -7 to the Riemann zeta function.

Cool. We dealt with all the positive integers, or the negative integers of the Riemann zeta function. What about the reciprocals of sums of integer powers? Technically, we already have a head start into figuring these sums out. Recall the work done to get to this formula:

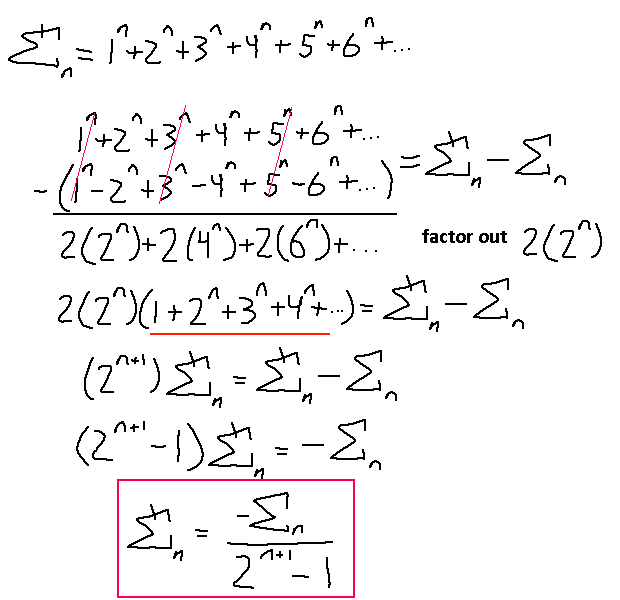
Notice how we didn't assume anything about the nature of n. We simply cancelled terms out and found our original sequence again to reduce the problem down. This means that this relation will still hold for n's smaller than 0, or for fractions, or for complex numbers! Probably. Yeah.

Unfortunately, our methods of solving these types of alternating terms aren't going to work the way they worked with the powers of integers. We'll have to be a little more clever. Trust me, I tried a lot. Let's solve for when n = -1.

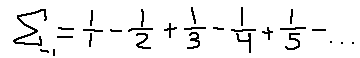
Hmm. This looks familiar, actually… is this some kind of Taylor series of a known function?

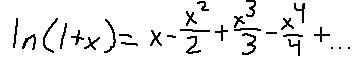
Ahh! Looks like the work was done for us! For those that don't know, a Taylor series is a really clever method of approximating many kinds of functions using only the power of polynomials. It is an approximation that's only really accurate over a small domain, but this will work for us. As you may see, if we set x = 1, we end up with exactly the sequence we are looking for, and it is equal to a finite value! Let's start plugging in things.

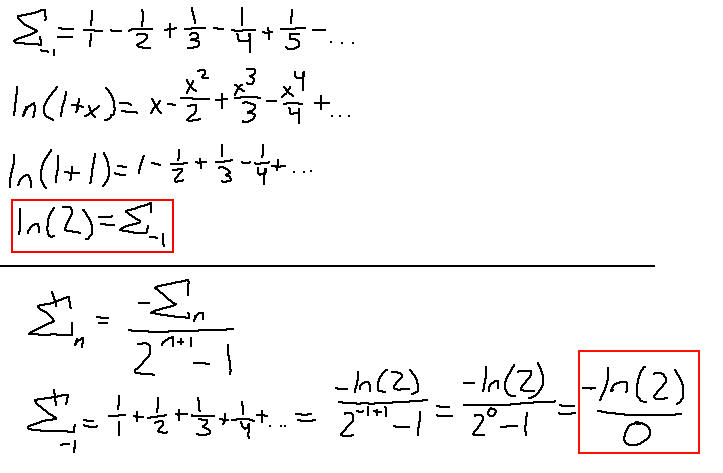
Oh… division by zero. I guess we're done here. Not even with this formula can we assign a value to an infinite series like this. Fun fact: this particular series has a name, called the Harmonic Series. It is a popular infinite series that is known to diverge. Still, all our other ridiculous series diverge, yet we were able to find a value for them… Oh well.

Maybe we'll get more luck with the next one? Set n = -2 and see if we can get lucky twice.

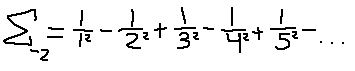
It kind of looks like the taylor series for the natural logarithm function. I have an idea. Let's assume that it is of some form of the taylor series of the log, and start at the taylor series and work our way to our desired alternating series.

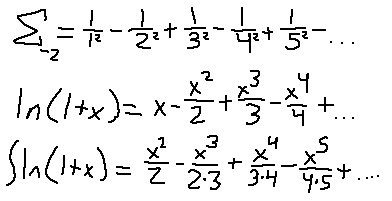
Darn… so close. What I did was integrate both sides of the taylor series definition with respect to x. For some x^N attempting to integrate it will give you x^(N+1) / (N+1), so that's where those extra constants came from in all the denominators. If only all those terms had the same constants multiplied by each other down there, then they would be square numbers and we'd be really close to our desired series.

All the new denominator factors are just one too high. However, if I factor out an x from every term beforehand, that would reduce the powers of all the terms by 1, and therefore reduce the factors in the denominators by 1 when we perform the integration!

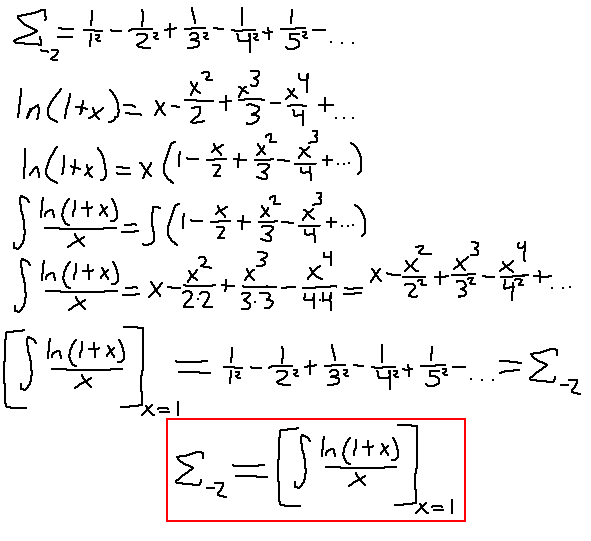
Nice. All we have to do now is integrate that function successfully, then set x = 1 (no, we can't set x = 1 first).

Uhm. Hmm. That's not really a nice function to integrate. It is in fact, not possible to integrate using ordinary methods. I had to look up for possible solutions to this and apparently what this resolves to is something called a Polylogarithm.

Unfortunately this is as far as I was able to go down this path. Despite not having a nice conclusion I am posting this anyway as there is still some useful knowledge behind this. At the very least, a small subset of the Riemann Zeta function was derivable, if you would even count this as a derivation.