Finding Squares, Generalized
Imagine a square composed of smaller, 1 unit squares. This square is size N x N. Given this current information, how can one find a square whose length is one larger? Well, if our original square is N x N, then this unknown square is (N + 1)(N + 1). That distributes out to N^2 + 2N + 1. Here’s a diagram showing the two squares.
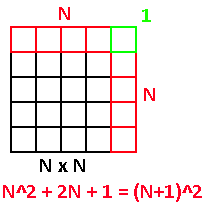
Makes sense so far. So if we already know the value of N^2 and just want the additional part that makes of (N+1)^2 all we do is subtract N^2 from N^2 + 2N + 1 to get 2N + 1. If we want to know how to get 6x6 from a 5x5 square, just add 2(5) + 1 to 5x5 to get 25 + 10 + 1 = 36.
Generalizing this is also easy. To get from an N^2 to an (N+H)^2 square where H can be anything (even negative), do the same subtraction method.
(N+H)^2 - N^2 = N^2 + 2HX + H^2 - N^2 = 2HX + H^2
If we start from a square of 0 length and figure out how to get a square of N length (so N = 0 and H = N) then we get N^2 as a result, which makes sense.
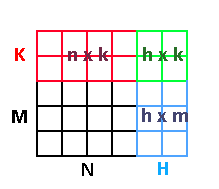
Let’s step it up a notch. How about a rectangle? Instead of N^2 we now have N * M lengths. We can arbitrarily change two dimensions in different ways now, so now we could have a rectangle changing to a size (N + H)(M + K). Here’s the new setup now:
NM + NK + HM + HK - NM = NK + HM + HK
Okay, so it’s still reducible but now it just looks like alphabet soup. Here’s a picture instead.
Still not bad. How about something a little less…. four-sided.
The unit triangles are equilateral and have a side length of 1. Increasing this triangle’s size will now mean adding another row to the bottom, like so:
I’m considering the black triangle a size 2 and the black and red combination a size 3. What’s cool (or rather boring) is that this triangle grows at the same rate the square does. That is, an N size triangle is N ^ 2 units large.
size 1 = 1 triangles
size 2 = 4 triangles
size 3 = 9 triangles
Finding a triangle of size (N + H) from size N is going to give the same results as the square. What we should do instead is to add another dimension.
Meet the cube.
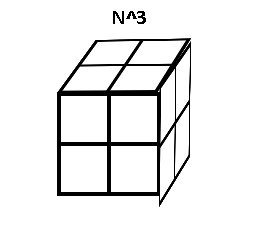
It’s hard to make cubes. Anyways, with a new dimension, the total volume is now N^3. We want to find (N+1)^3. Distribute that term out and subtract by N^3 and you get this:
N^3 + 3N^2 + 3N + 1 - N^3 = 3N^2 + 3N + 1
Here is a graphic showing what’s going on for a 2x2x2 cube to a 3x3x3 cube.
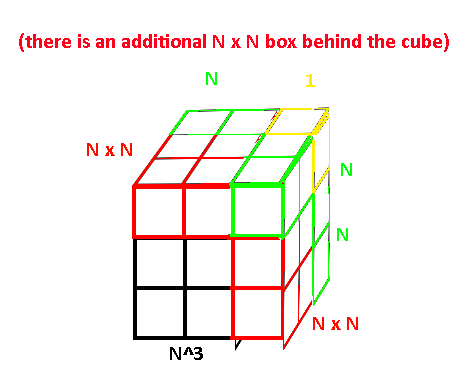
For an arbitrary amount, this equation will be (N + H)^3 - N^3, or
N^3 + 3HN^2 + 3NH^2 + H^3 - N^3 = 3(H)(N^2) + 3(H^2)(N) + (H^3)
If we allowed stretching the cube in three different directions with different amounts, then this gets stupidly hard to understand, so let’s stick with just scaling all parts of a cube equally and instead start scaling up to another dimension to get a hyper-cube. No, you are not getting a drawing of this one. This is the difference equation now for scaling by 1 and by an arbitrary amount.
(N+1)^4 - N^4 = N^4 + 4N^3 + 6N^2 + 4N + 1 - N^4 = 4N^3 + 6N^2 + 4N + 1
(N+H)^4 - N^4 = N^4 + 4(N^3)(H) + 6(N^2)(H^2) + 4(N)(H^3) + H^4 - N^4 = 4(N^3)(H) + 6(N^2)(H^2) + 4(N)(H^3) + H^4
Note that the coefficients in this term is 4,6,4,1. The full sequence is 1,4,6,4,1 but the N^4 removed that first 1. This is in fact the values of the 5th row of pascal’s triangle. For N^3 it has similar coefficients of 3,3,1 (it would’ve been 1,3,3,1 but N^3 removed the first 1). We can find a specific term’s coefficient by looking it up in pascal’s triangle via the combinatoric function.
Now for the final test. Given a hyper-cube of dimension D, and an increase of size by H, what is the formula for finding that difference? Here is the equation to solve:
(N + H)^D - N^D
We know that the - N^D will cancel out a term easily, so let’s ignore that for now. Remember, the coefficients can be found by using the combinatoric function which I will now display as C(n, k).
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
Here are some example uses of C(n, k).
C(3,2) is for the row ‘1 3 3 1’, and finding the element in position 2 (we count from 0), so that would be the right-most 3 in the triangle
C(2,1) is for the row '1 2 1’ and finding the element in position 1, so 2.
C(4,4) is for the row '1 4 6 4 1’ and finding the element in position 4, so the rightmost 1.
This will be useful when finding out the coefficients. We know that for dimension D, we must use C(D, k), where the k value will change depending on what term we are on. This is actually enough to help expand (N + H)^D out so that we can get an idea of the answer.
(N + H)^D = C(D, 0)(N^D)(H^0) + C(D, 1)(N^(D-1))(H^1) + C(D, 2)(N^(D-2))(H^2) + ... + C(D, D-1)(N^1)(H^(D-1)) + C(D, D)(D^0)(H^D)
There’s not exactly a better way to showcase this expansion, I’m afraid. We can see some patterns, however. The N term starts at N^D and D decreases down to 0. The H term starts at H^0 and the 0 increases to D. The combinatoric goes from C(D, 0) to C(D, D). We can use a summation to help compress this theoretically infinitely long answer! Here’s my made up notation.
(N + H)^D = Summation, starting from i = 0 to i = D —> C(D, i)(N^(D - i))(H^i)
Oh yeah, don’t forget to subtract the N^D term. Evaluating this C(D, i)(N^(D - i))(H^i) term at i = 0 actually gives us this:
C(D, 0)(N^D)(H^0) = 1(N^D) = N^D
So, to remove that value, simply start the i increment at i = 1.
(N + H)^D - N^D = Summation, starting from i = 1 to i = D —> C(D, i)(N^(D - i))(H^i)
Whoops, this was supposed to be a simple post…