Angles! Circles! Integrals!
One thing that was always strange to me is that finding the arc length of a circle depends on a multiplication of the radius of the circle and the total angle the arc spans. Multiplication of two values usually geometrically represents a rectangular area with widths and lengths of the two values. In this case, it represents the length of a one-dimensional line. It was then that I decided to dig deeper into this. The following is the result of my findings.
To make things more intuitive to understand, I will be using Tau (τ) which is equivalent to 2 Pi. One Tau therefore is one revolution of a circle. Sorry, not sorry, Pi lovers.
Firstly, let me start by saying that both diagrams below are equally valid representations of the multiplication of the radius and of Tau:
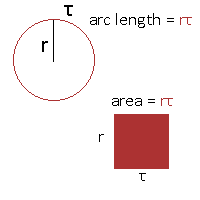
The roles of the radius and Tau can even swap (as it should: multiplication is commutative, after all). See below, where 2 becomes the arc in radians and Tau the radius of the circle. Both red lines should have the same length.

The Area of a Circle is...
The formula for the area of a circle in terms of Tau is (1/2)(Tau)(radius)^2. Note the 1/2 term, which makes this different than the usual (Pi)(radius)^2. The one-half term tells us something though.
Let's compute the area using many small pie slices of the circle and add them up. That's right. It's integration time.
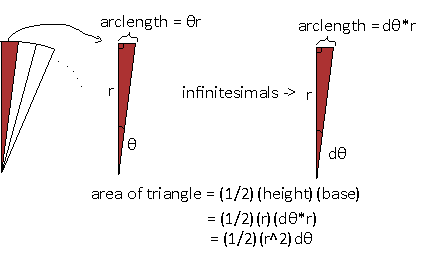
In the world of infinitesimals, we take tiny bits of angles, as close to 0 as possible. When taking such a small slice like this, the curve at the top of the slice tends to become flat, and we can actually treat it as flat. This means we have a right triangle here, and it is easy to compute the area of a right triangle. dθ is that infinitesial angle, and to handle all the infinitely many, infinitely small slices, we need to use integrals to sum them up in one sweep.
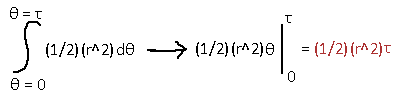
We want to compute all the triangles around the circle, which means the range of integration is from 0 radians to Tau radians. Going through the integral, we get back our area for a circle. That was easy. So, the one-half comes from the areas of the infinitesimal triangles! But we didn't even need to bring calculus into this! Watch as I organize the infinitesimal triangles into another shape:
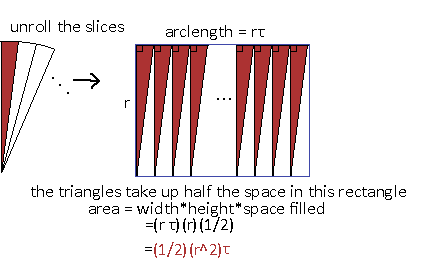
All the lined up triangles with their top edges aligned makes the circumference of the whole circle, the top of the rectangle. The radius is the side of the rectangle. No angle is even needed here other than Tau. Simple. Beautiful.
More Shapes
What happens if we try an alternate representation of the area of a circle? Remember the first point that multiplication could be represented as arclengths. So we could use one of the radii and Tau in the area formula to make an arclength. Here's what that would look like:

The red circle in front is the arclength of the red terms in the expression. Then the blue colored radius is multiplied to the result, creating a cylinder shape (without the flat parts) out of the circle by extending the radius out to the third dimension. Finally, the surface area is cut in half by the black term, leaving just the blackened surface area of the cylinder as the total area. This area is the same area of the circle of radius r!
It would have been too ugly to show, but you could have also started with a length of r (the radius), then multiply it by the arclength (r*τ), making what looks like a toilet paper roll (like how the black shaded part in the image above is). Then the half would cut that roll in half, giving the same area.
Using Exponentials
Exponentials do that thing with circles, right? Where does e^(i*Pi) = - 1 fit into all this? Firstly, e^(i*θ) finds a specific point on a unit circle at angle θ. If we want to use this to find arclengths we need to make a differential out of this expression by measuring two of these points and finding the difference between them, and making sure to squeeze the two points infinitely close together, such that the line segment they make lines up exactly with the circle's perimeter.
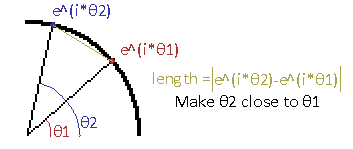
θ2 will basically be θ1 but with an infinitesimal change. So another way to write this is θ2 = θ1 + dθ, where dθ is the infinitesimal change that makes θ2 different from θ1. Cleaning up the terms a bit and integrating from the angle of 0 to Tau (the full circle), we get the sum of all these infinitely tiny lengths around the circle and get this abomination:
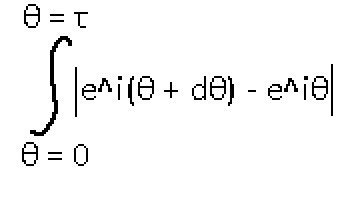
Those lines surrounding the expression are absolute symbols. See, the difference result will actually be a complex number, so I'm taking the magnitude of it since we don't care about the angles of the line segments when doing the integral. An infinitesimal inside an exponential is kind of a problem. This was definitely not in my calculus homework. How about tackling this by hand? Let's plug in some theta values and just see what happens to the output.
| θ | dθ | Magnitude of e^i(θ+dθ) - e^i(θ) |
|---|---|---|
| 1 | 1 | 1 |
| 1 | .5 | .5 |
| 1 | .01 | .01 |
| 1 | 1000 | 1000 |
Huh... it seems that the only factor that matters is dθ. Even better, the resulting difference seems to exactly be dθ! Let's substitute the nasty expression earlier with dθ.
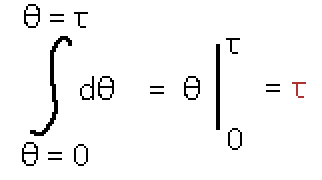
This makes sense. The sum of all the line segments should give us back the arclength, and since we were dealing with a unit circle the radius is 1, which is why Tau is all on it's own. Neat.